Определение координат точек теодолитного хода
Разомкнутый теодолитный ход должен начинаться и заканчиваться на опорных точках H и К с известными координатами, и на этих точках должны быть измерены примычные углы β0 и βn между опорными линиями с известными дирекционными углами и первой и последней линиями хода. Только в этом случае имеется возможность не только определить координаты всех точек теодолитного хода, но и проконтролировать правильность измерения углов и сторон хода и оценить точность выполненной работы. Если разомкнутый теодот литный ход имеет исходные данные только с одной стороны (в начале или конце хода), то его называют висячим теодолитным ходом.
Для контроля целесообразно в начальной и конечной опорных точках измерять не по одному, а по два примычных угла, т. е. независимо дважды определять дирекционный угол сторон HI от опорной линии АН и опорной линии СН, а в конечной опорной точке определять дирекционные углы опорных линий KB и КД и сравнивать полученные и известные их значения.
В замкнутом теодолитном ходе (рис. 1.16) обычно измеряют внутренние углы полигона (β1,...,βi,) и примычные углы β'0,β"0" . Необходимость привязки замкнутого хода к двум твердым линиям связана с тем, что при ошибочном опознавании, например пункта А, дирекционный угол линии АН не будет соответствовать его действительному значению и весь полигон будет неправильно ориентирован относительно принятой системы координат. Поэтому для исключения такой ошибки необходимо делать привязку хода как минимум к двум опорным линиям.

Рис. 1.16. Схема замкнутого и диагонального теодолитных ходов
Внутри замкнутого хода можно проложить диагональный ход, опирающийся на вершины основного хода (на рис. 1.16 ход 6-8-9-2).
В разомкнутом (рис. 1.14) и замкнутом (рис. 1.16) теодолитных ходах кроме необходимых для определения координат точек хода измерений выполнены избыточные измерения: в разомкнутом ходе избыточными являются примычные углы βn, β'n ; угол βn-1 и сторона dn, а в замкнутом — углы β6, β7 и d7, что позволяет выполнить уравнивание и оценку точности этих ходов.
Известно, что каждое избыточное измерение приводит к условному уравнению, в рассматриваемом случае имеем три избыточных измерения, которые дают одно условное уравнение фигуры и условные уравнения абсцисс и ординат.
В теодолитном ходе угловая невязка (свободный член условия фигур)
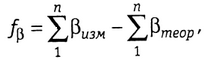 (1.12)
(1.12)
где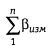 - сумма измеренных в
теодолитном ходе углов, а
- сумма измеренных в
теодолитном ходе углов, а 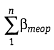 -
их теоретическая сумма. В замкнутом теодолитном ходе с n
измеренными углами, как известно из геометрии
-
их теоретическая сумма. В замкнутом теодолитном ходе с n
измеренными углами, как известно из геометрии
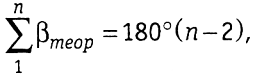 (1.13)
(1.13)
следовательно, в замкнутом теодолитном ходе
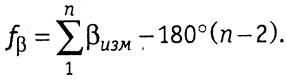 (1.13)
(1.13)
В разомкнутом теодолитном ходе теоретическая сумма углов зависит от
расположения исходных сторон, и поэтому целесообразно разомкнутый ход превратить
в замкнутый путем продолжения опорных линий до их пересечения и использовать его
для определения 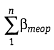 .
.
На рисунке 1.14 для измеренных левых углов имеем
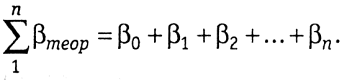
В полученном замкнутом полигоне сумма углов
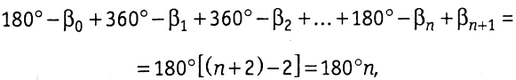
где n — число измеренных углов. Из этого выражения находим
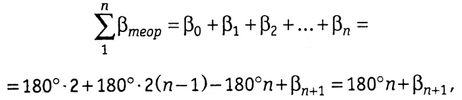
т. е. в рассматриваемом случае, учитывая
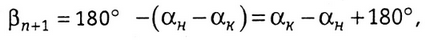
получаем
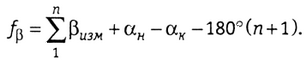
На рисунке 1.17
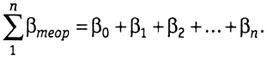
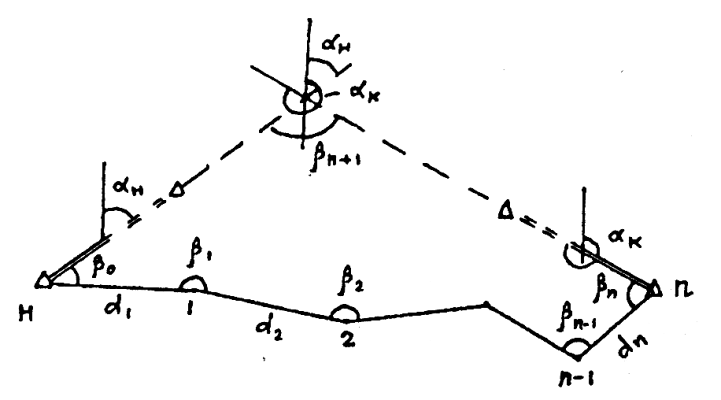
Рис. 1.17. Схема разомкнутого теодолитного хода
В полигоне
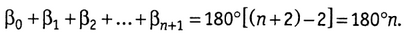
Учитывая βn+1= 360° - (ак-ан), находим
a
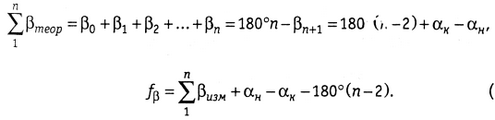 (1.15)
(1.15)
Если ошибки угловых измерений носят случайный характер и значения mβ1 ≈ mβi ≈ mβ то, используя формулу (1.13) и формулу средней квадратической ошибки функции, имеем
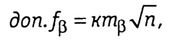 (1.16)
(1.16)
де к — коэффициент перехода от средней квадратической ошибки к предельной. При к = 2, mβ = 30"
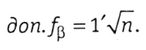
Если фактическая ƒβ, вычисленная по формулам (1.13)—(1.15), по модулю меньше доп.ƒβ, то ее распределяют с обратным знаком поровну на все измеренные углы, т. е. поправка
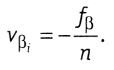 (1.17)
(1.17)
Если невязка ƒβ не делится без остатка на число n, то несколько большие поправки вводят в углы с короткими сторонами. В итоге сумма поправок, лолжна оавняться угловой невязке ƒβ с обратным знаком, т.е.
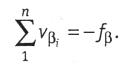
После введения в углы βi поправок vβi получают исправленные углы, которые используют при вычислении дирекционных углов по формуле (1.10) для левых и по формуле (1.11) для правых измеренных углов. При этом дирекционный угол конечной опорной линии, вычисленный по теодолитному ходу, и его истинное значение должны совпадать. В замкнутом ходе дирекционные углы опорных линий НА и НВ (рис. 1.16) после вычисления теодолитного хода также должны совпадать с их известными значениями. После определения дирекционных углов вычислют приращения координат
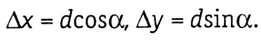
Вследствие ошибок при измерении углов и сторон 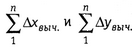 не совпадают с их теоритическими
значениями
не совпадают с их теоритическими
значениями 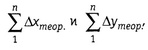 т.е. невязки по
осям координат
т.е. невязки по
осям координат
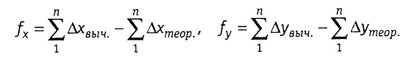
Для определения 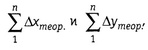 имеем
имеем
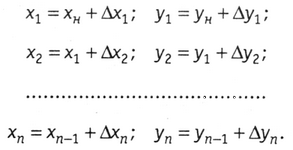
Сложив левые и правые части полученных выражений, находим
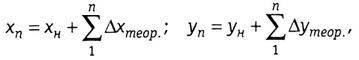
откуда
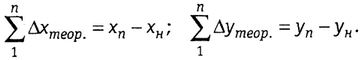
С учётом полученных значений
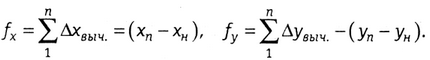 (1.18)
(1.18)
В замкнутом теодолитном ходе начальная и конечная точки совпадают, поэтому хn = xн, уn = yн, а вместо формулы (1.18) Имеем
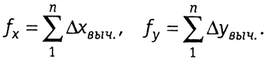
Вследствии невязок ƒх, ƒy положение конечной опорной точки, полученной по теодолитному ходу, не будет совпадать с положениеми опорной точки, величина этого несовпадения, называемая невязкой в периметре хода,
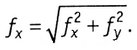
Отношение ƒs к периметру хода 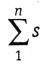 ,
т. е. называют относительной невязкой в периметре хода, она характеризует
качество полевых работ и не должна превышать установленной величины.
,
т. е. называют относительной невязкой в периметре хода, она характеризует
качество полевых работ и не должна превышать установленной величины.
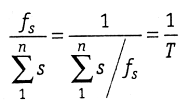
При измерении длин сторон лентой или дальномерными насадками ДНТ, ДАР-100 щШ ДД-3 при неблагоприятных условиях
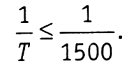
При благоприятных условиях измерений относительная невязка может быть 1:2000 и даже 1:3000.
В тахеометрическом ходе при измерении сторон нитяным дальномером
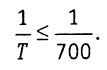
Если относительная ошибка допустима, то в приращения координат вводят поправки
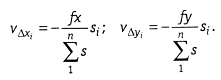 (1.9)
(1.9)
Суммы поправок должны быть равны соответствующим невязкам по осям с обратным знаком, т. е.
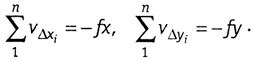
Исправленные значения приращений координат используют для определения координат точек хода по формулам
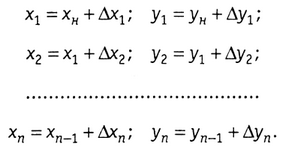
В результате хn, уn в разомкнутом и хn = x, yn = yн в замкнутом и ходах должны совпадать с их известными для опорных точек значениями.
Пример вычисления координат пунктов разомкнутого теодолитного хода приведен в таблице 6. Схема хода изображена на рисунке 1.18.
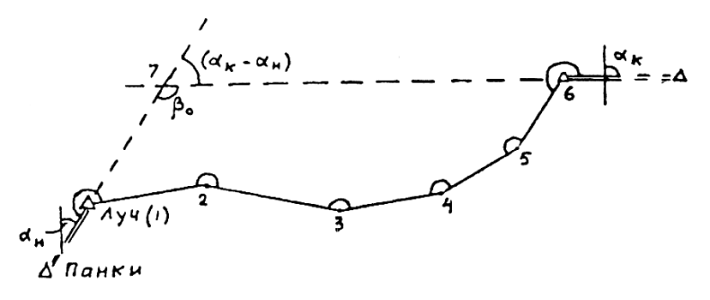
Рис. 1.18. Схема теодолитного хода
Таблица 6
| Пункты | Углы поворота (левые) |
Дирекцинные углы а |
Горизонтальные проложения, м |
Δх = dcosα,м | Δу = dsinα, м | Координаты, м | |
| x | y | ||||||
| Панки | 0,0 | ||||||
| 46° 18,2' | |||||||
| Луч(1) | 181° 15,6' | +4 | -1 | 5141,15 | 819,31 | ||
| 0,0 | 47° 33,8' | 93,45 | +63,06 | +68,97 | |||
| 2 | 247° 18,4' | +4 | -1 | 5204,25 | 888,27 | ||
| 0,0 | 114° 52,2' | 154,12 | -64,82 | +139,83 | |||
| 3 | 119° 38,9' | +4 | -1 | 5139,47 | 1028,09 | ||
| 0,0 | 54° 31,1' | 121,85 | +70,73 | +99,22 | |||
| 4 | 155°12,3' | +4 | -2 | 5210,24 | 1127,30 | ||
| +0,1 | 29° 43,4' | 114,19 | +99,17 | +56,62 | |||
| 5 | 161° 46,3' | +4 | -2 | 5309,45 | 1183,90 | ||
| +0,1 | 11° 29,8' | 89,55 | +87,75 | +17,85 | |||
| Лес (6) | 254° 45,3' | 5397,24 | 1201,73 | ||||
| 86° 15,2' | |||||||
| Ужово | |||||||
|
Σβизм. = 1119º56,8' Рм = 573,16м |
Σ∆хвыч. = +255,89 | Σ∆увыч. = +382,49 | |||||
| Σβ тсор. = 180° (7-2) + 180°- [180° - (αк — αн)] = 1119°57,0' | Σ∆хтсор. = +256,09 | Σ∆хтсор. = +382,42 | |||||
| ƒр = Σβ изм. - Σβ тсор. = -0,2' | fx = -0,20 | fy = +0,07 | |||||
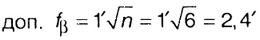 |
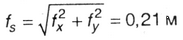 | ||||||
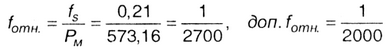 | |||||||

